Reading in From a File to a Binary Search Tree Using Linked Stack

LookFar Labs28 July 2016

How and When to Implement Binary Search Copse

No, they're non just something you'll get asked about in tech interviews

If the patterns you write in your code are non efficient, yous are stealing time from your users and in essence, draining them of their precious life force. If "programmer" secretly meant "code vampire" this would exist fine; but as information technology stands, wasteful code accomplishes goose egg beyond annoying your users. Use efficient lawmaking, and don't steal life forcefulness!

How many times have you written this construction?

var searchKey = "john"

for(elem in assortment) {

if(elem.name == searchKey) {

// DO SOMETHING

break;

}

}

This lawmaking gets the job done in a logical manner. I have a list of elements and each one has a name property, so to find the one I want, I'll only run through the whole list until I discover the i that matches.

All the same, this is Non the most efficient way. Occasionally, the element you lot are looking for volition be at the beginning of the array, but only as often, it volition exist at the end. This isn't a big deal for an array of 10 or 20 elements, merely what about k, 10000, or 1000000? How tin can nosotros bring down the average time the computer spends looking for the correct element? At that place are many techniques to accomplish this, only today we are going to wait at the applications of the Binary Search Tree.

When to Use Binary Search Trees

Implementing a binary search tree is useful in any state of affairs where the elements can exist compared in a less than / greater than manner.  For our example, we'll use alphabetical society as our criteria for whether an element is greater than or less than another chemical element (eg. "alan" < "bob" < "dave" < "john" < "kyle" < "leonard" < "zack").

A tree is a set of information elements connected in a parent/child design. For instance:

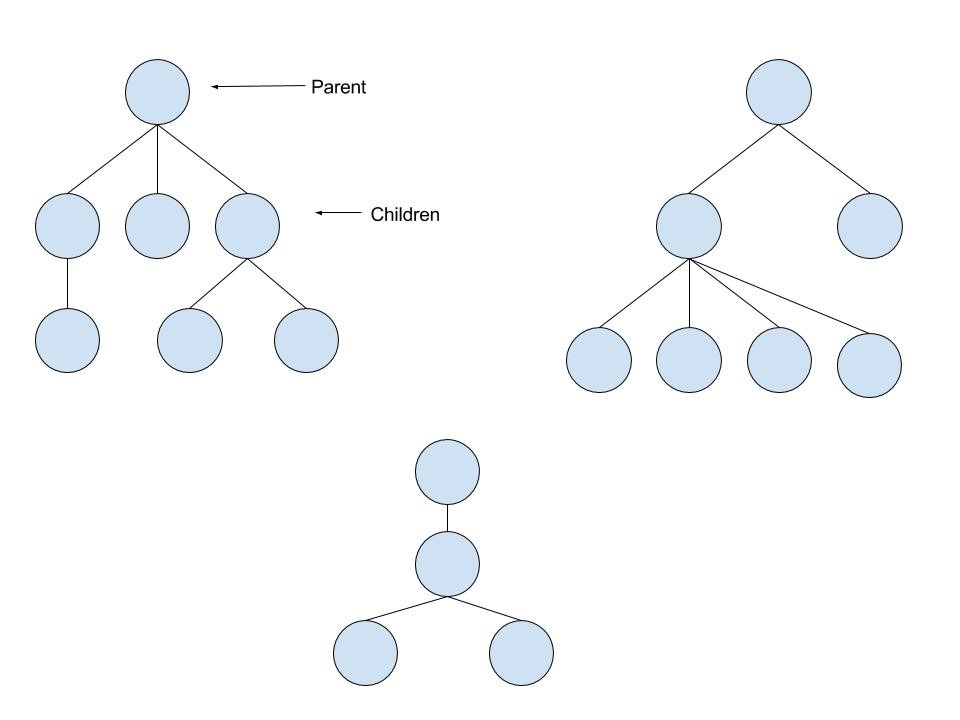
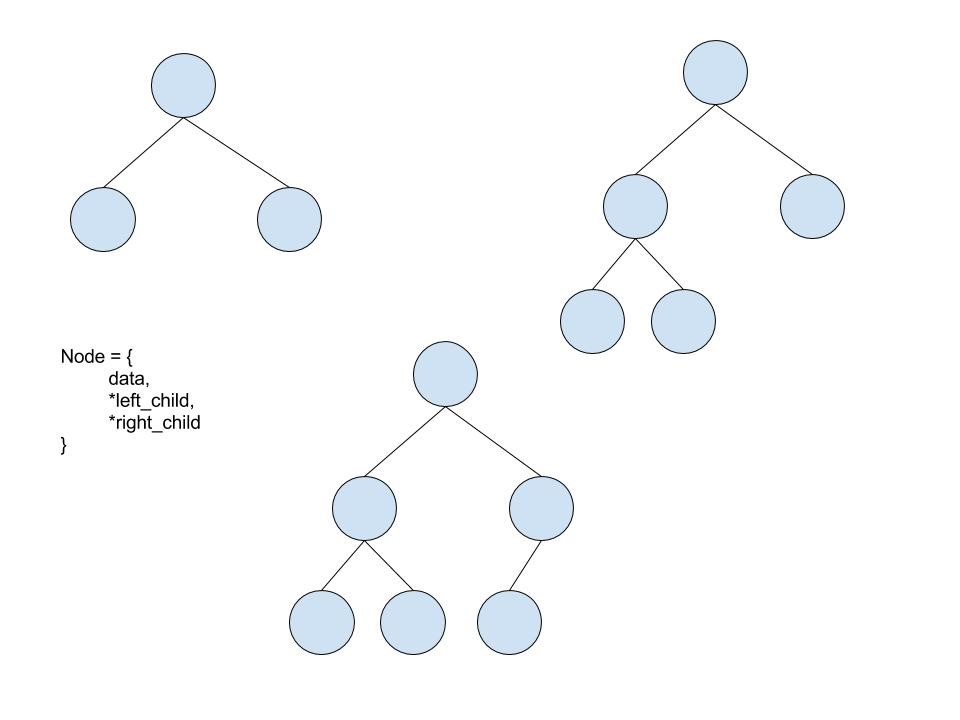
A binary tree is a tree construction in which each data element (node) has at most ii children.

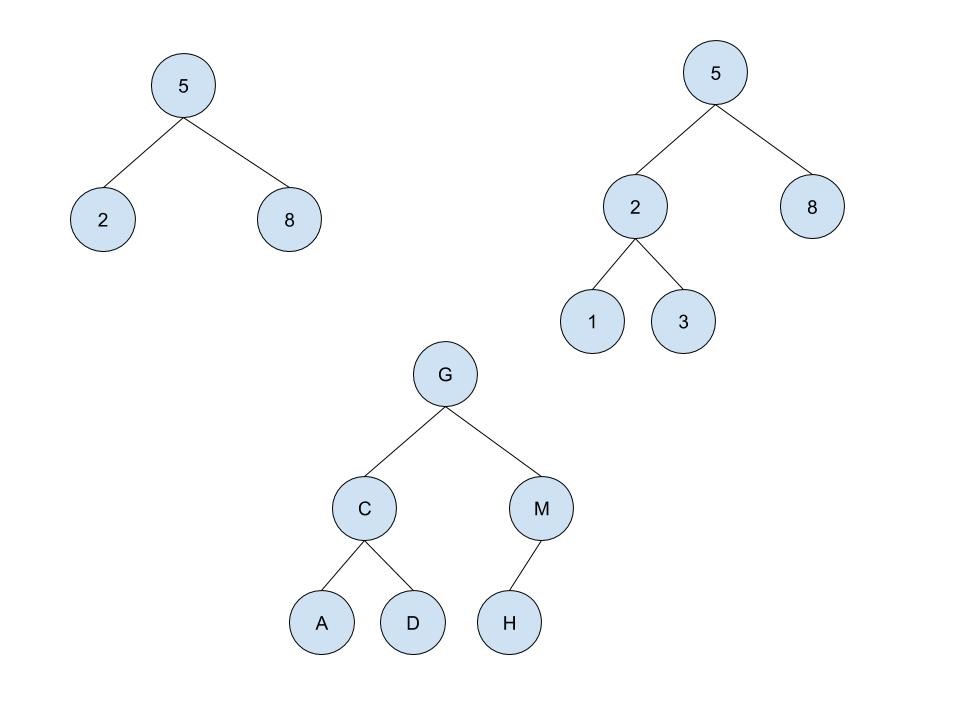
A binary search tree is a binary tree in which any child node or subtree to the left is less than the parent node, and any kid node or subtree to the right is greater than the parent node. Hither's a handy visualization:

Great! So why does any of this matter? Well, let'south encounter how nosotros would search.

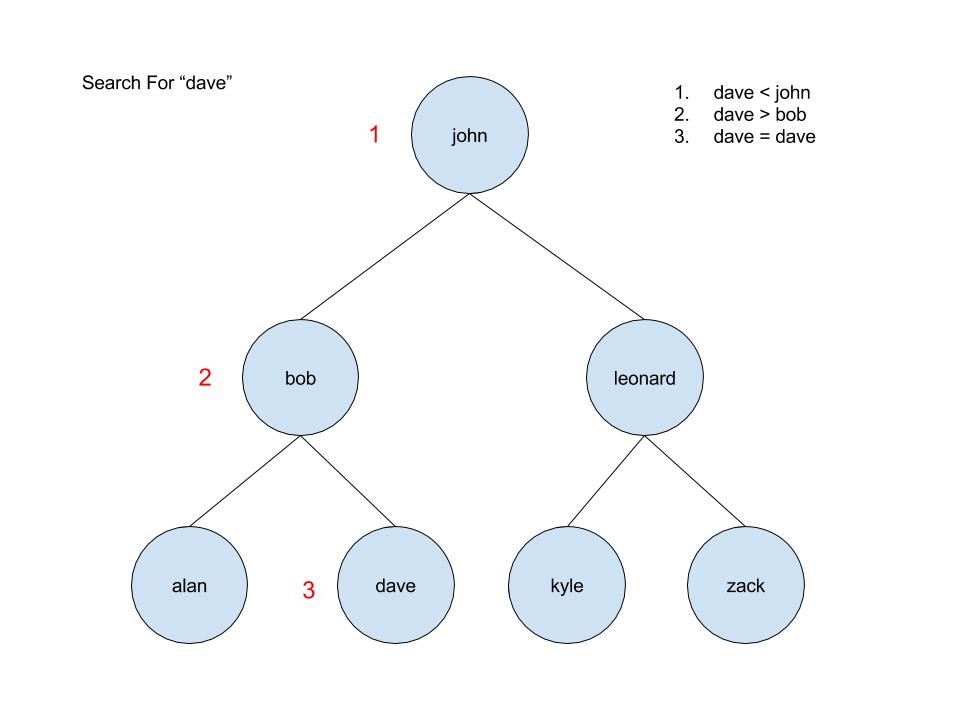
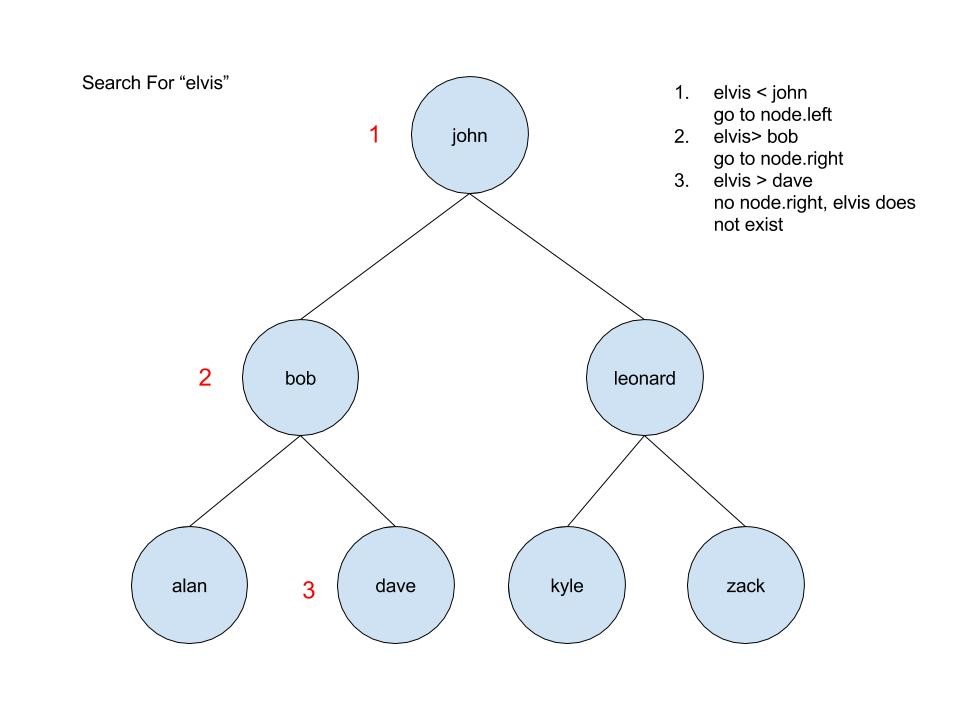
Start at the root. If the search key is less than the alphabetize primal of the chemical element, go to the left child. If the search key is greater than the index primal of the element, go to the correct child.

This process continues until the search central matches the index key (and the element is found), or until the terminate of the tree is constitute (in which instance the element does not exist). In iii comparisons, nosotros have either found the element, or we tin can be certain that it does not exist. For the assortment, it volition have us 7 comparisons to go the same information, and the larger the array, the more fourth dimension nosotros will save by using a binary search tree.

So searching is definitely faster, but what most other operations? On average, a binary search tree will beat an assortment in the number of operations information technology takes to insert or delete an element. If you lot are inserting an element to the end of an array, all you have to do is put the data in the the first bachelor memory address myArray[myArray.length] (this is more akin to pushing onto a stack). Nonetheless, if you accept to insert at the beginning of an array, you will need to shift every element over. The same is truthful for deletion. If the chemical element is at the terminate (similar popping off a stack), then you simply change the stored length of the assortment. But if you lot delete the first element, all of the others will need to be shifted. Since the binary search tree does non crave its elements to be stored in a contiguous block of retentivity, inserting or deleting a node tin can exist done past simply adjusting some pointers. Call up that each node is a struct containing information and pointers to left_child and right_child.

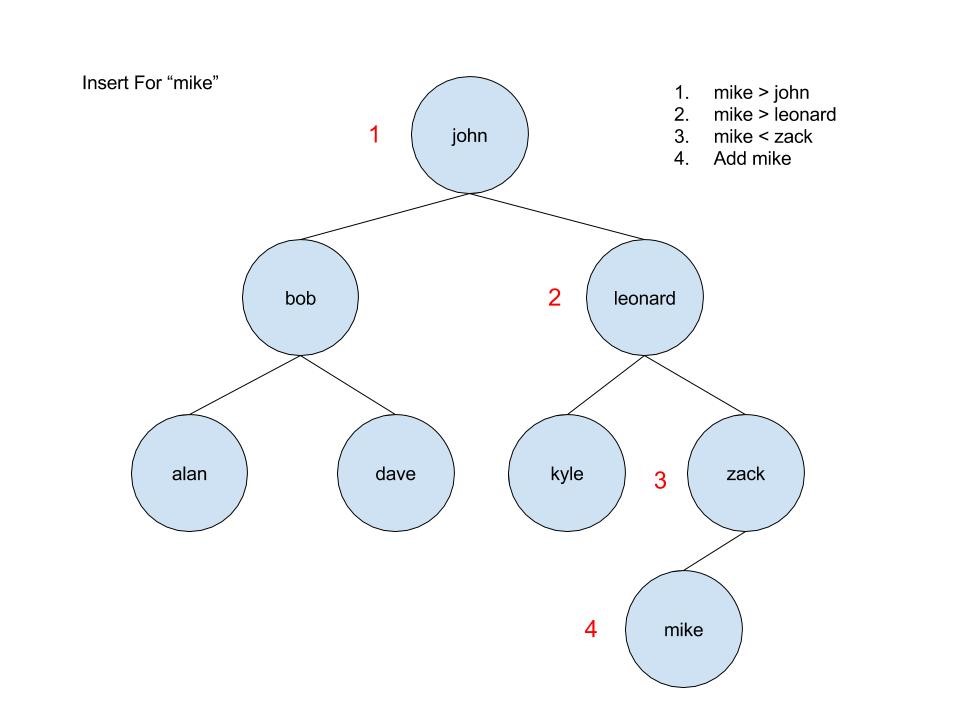
Then, why would I ever use an array?

A few reasons. One of the greatest advantages of using arrays is that element access tin be done in constant fourth dimension. For example, if you lot want to get the 5th element from an array, yous have the starting memory address and add (index * element_size). If our memory accost starts at 0 and this is an assortment of 8-bit characters, the 5th element would be at memory address 0+(iv*8) = 32. Information technology doesn't matter how many elements are in the array, this access fourth dimension remains abiding. If we were to use a BST in the aforementioned scenario there would exist no fashion to get to the 5th chemical element without starting at the root node and traversing to the fifth element. Also, since the tree is not a single-dimensional construct, you would need to define exactly what you mean by the "fifth" chemical element…and that introduces us to depth-outset vs breadth-starting time traversal (a large, big topic that we may cover at a afterward date).

Also, if your information is already in array class (maybe it was returned from the database in this mode), it is possible that the fourth dimension it would take to set up the BST the first time may accept longer than the worst instance search of that assortment. However, you take to consider whether you will be searching the array again and again. If that is the case, you lot may want to build your BST the first time and then use it for searches after that. Also, if your array is very, very long, it is probably worth it to use a BST.

Finally, let'due south talk about worst case scenarios for BSTs. What happens if the array is in alphabetical order and we build our BST?

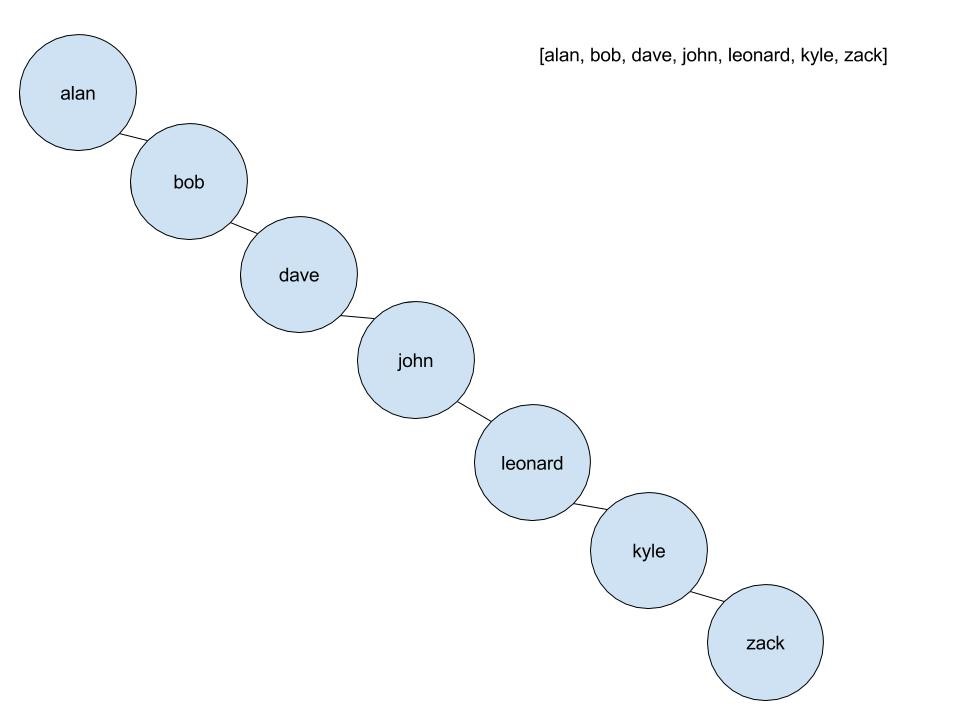
This is still a BST, but it is "unbalanced." In this state, a BST is reduced to its worst case, which is the same as an assortment for searches. In order to promote counterbalanced tree construction, the B-Tree and Red-Blackness Tree were invented. They are both special cases of the general binary search tree seen here, but they use a few balancing procedures to make certain y'all are gaining the total benefit of using a BST.

And that about covers the nuts! We'll be revisiting some of these concepts in the future, then stay tuned for some more in-depth coverage of comp sci topics.

phillipspreempory.blogspot.com

Source: https://www.lookfar.com/blog/2016/07/28/why-binary-search-trees-matter/

Share this post